Visualising your fitted non-linear dimension reduction model in the high-dimensional data space
Jayani P.G. Lakshika
Joint work with Prof. Dianne Cook, Dr. Paul Harrison, Dr. Michael Lydeamore, Dr. Thiyanga S. Talagala
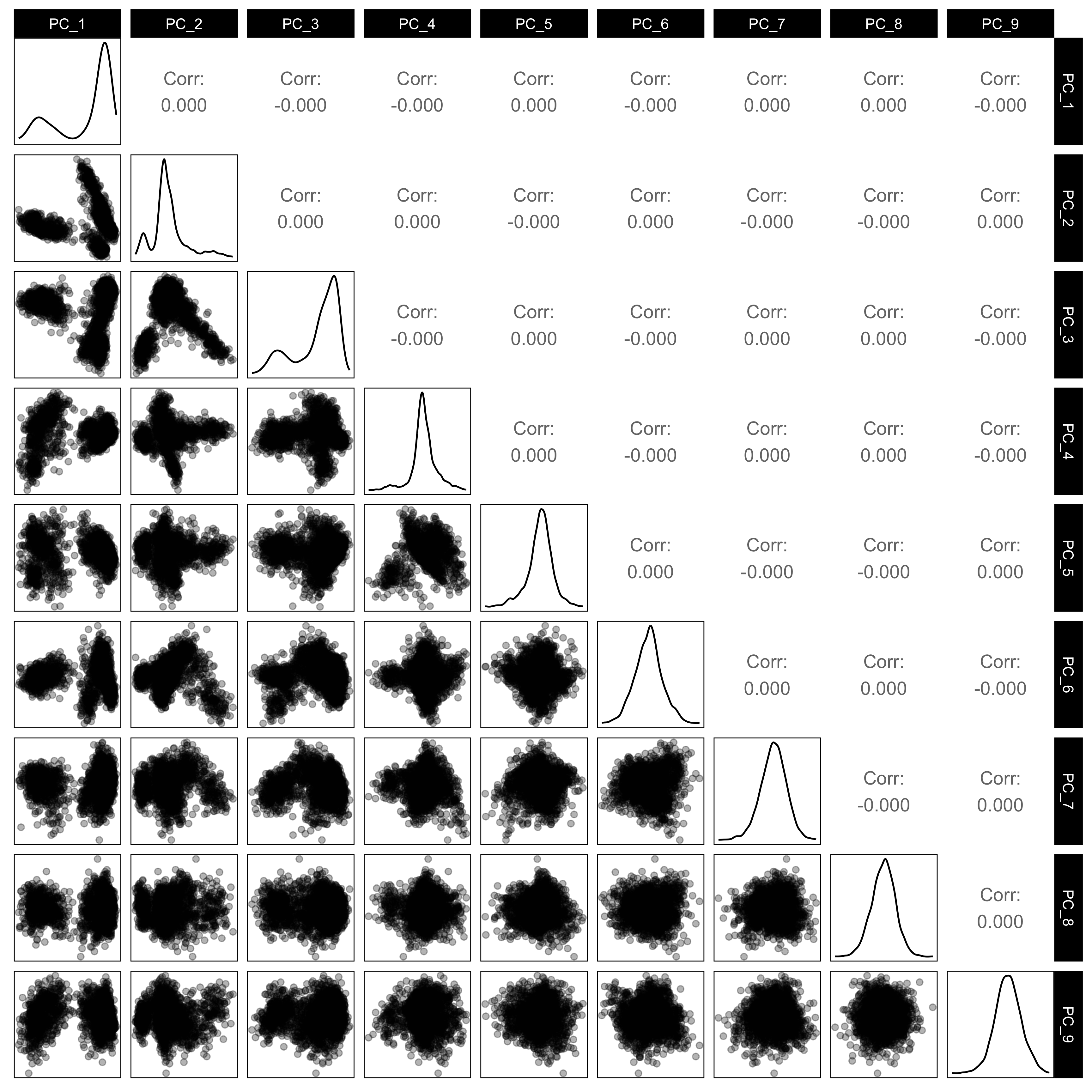
High-dimensional data
X=[x11x12⋯x1px21x22⋯x2p⋮⋮⋱⋮xn1xn2⋯xnp]
Peripheral Blood Mononuclear Cells (PBMC)
Tour
What is a tour?
- Interactive and dynamic graphics to visualise high-dimensional data.
Why is the tour technique employed?
Tour shows a sequence of linear projections as a movie.
It involves mentally assembling multiple low-dimensional views to comprehend the structure in higher dimensions.
Software: langevitour
Non-linear dimensional reduction (NLDR) techniques
NLDR techniques designed to capture the complex and non-linear relationships present within high-dimensional data.
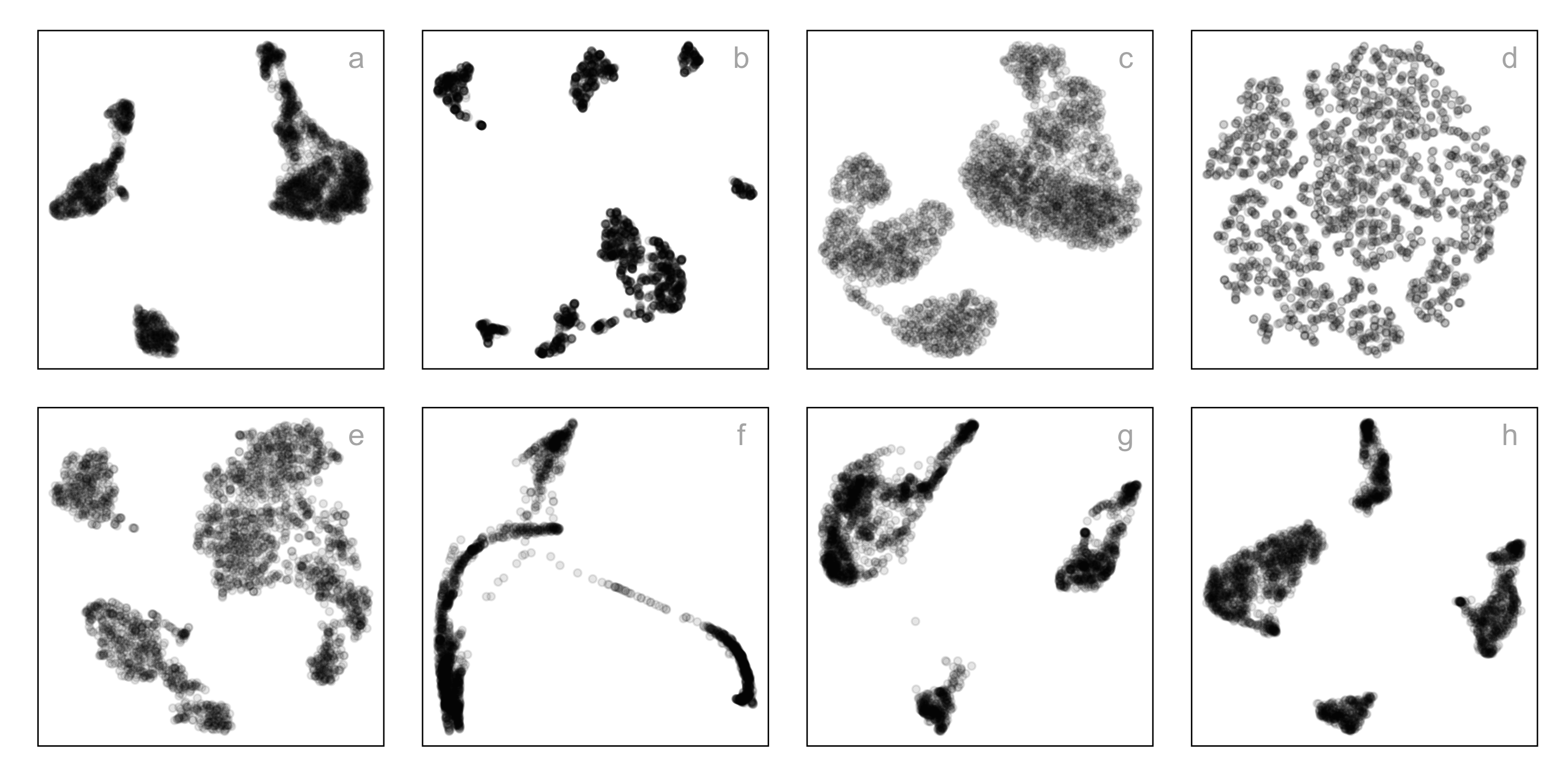
Match-a-roo (1/4)
The data shown in the two displays is the
- SAME
- DIFFERENT
Match-a-roo (2/4)
The data shown in the two displays is the
- SAME
- DIFFERENT
Match-a-roo (3/4)
The data shown in the two displays is the
- SAME
- DIFFERENT
Match-a-roo (4/4)
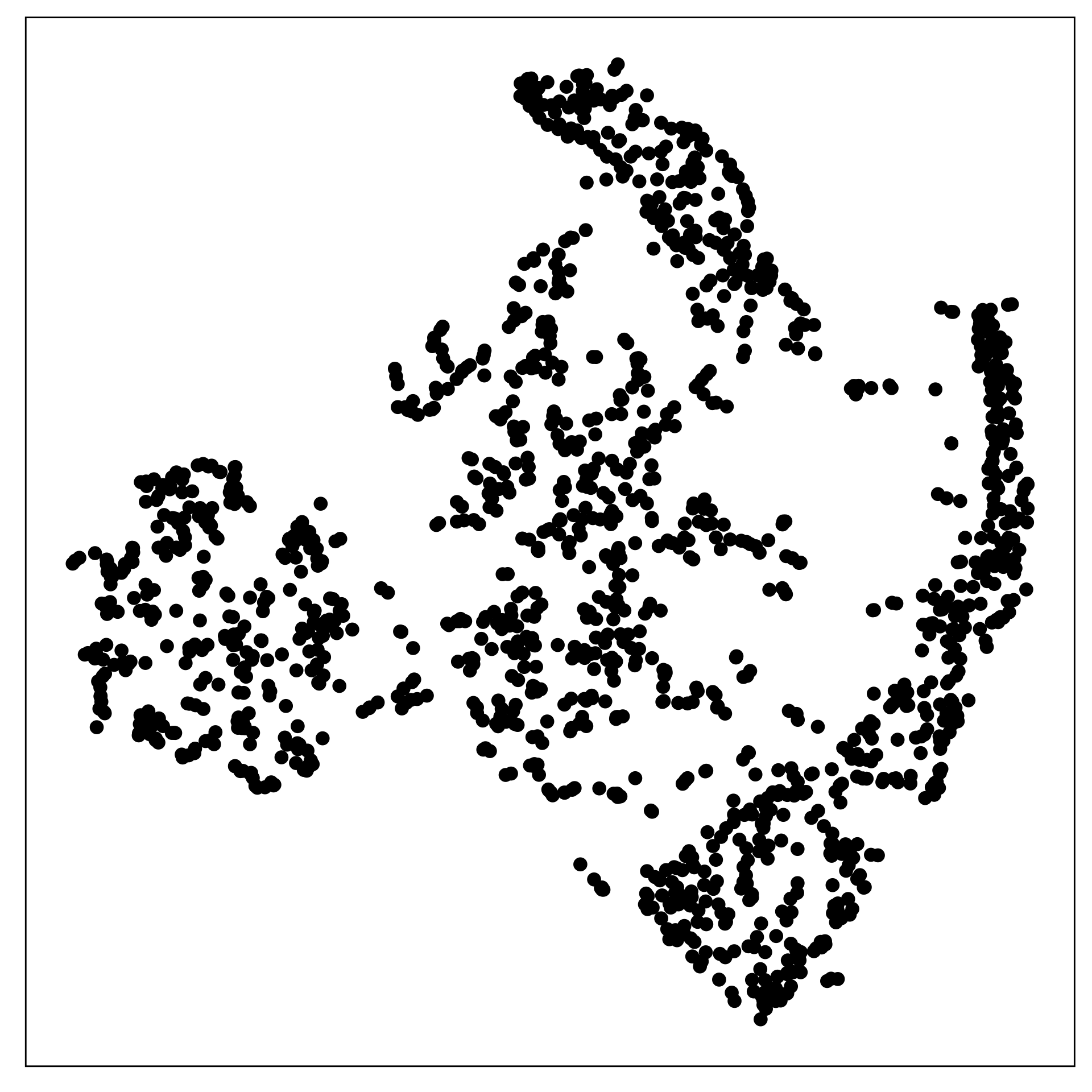
The data shown in the two displays is the
- SAME
- DIFFERENT
Motivation
Single-cell gene expression: same data, different NLDR + hyper-parameters
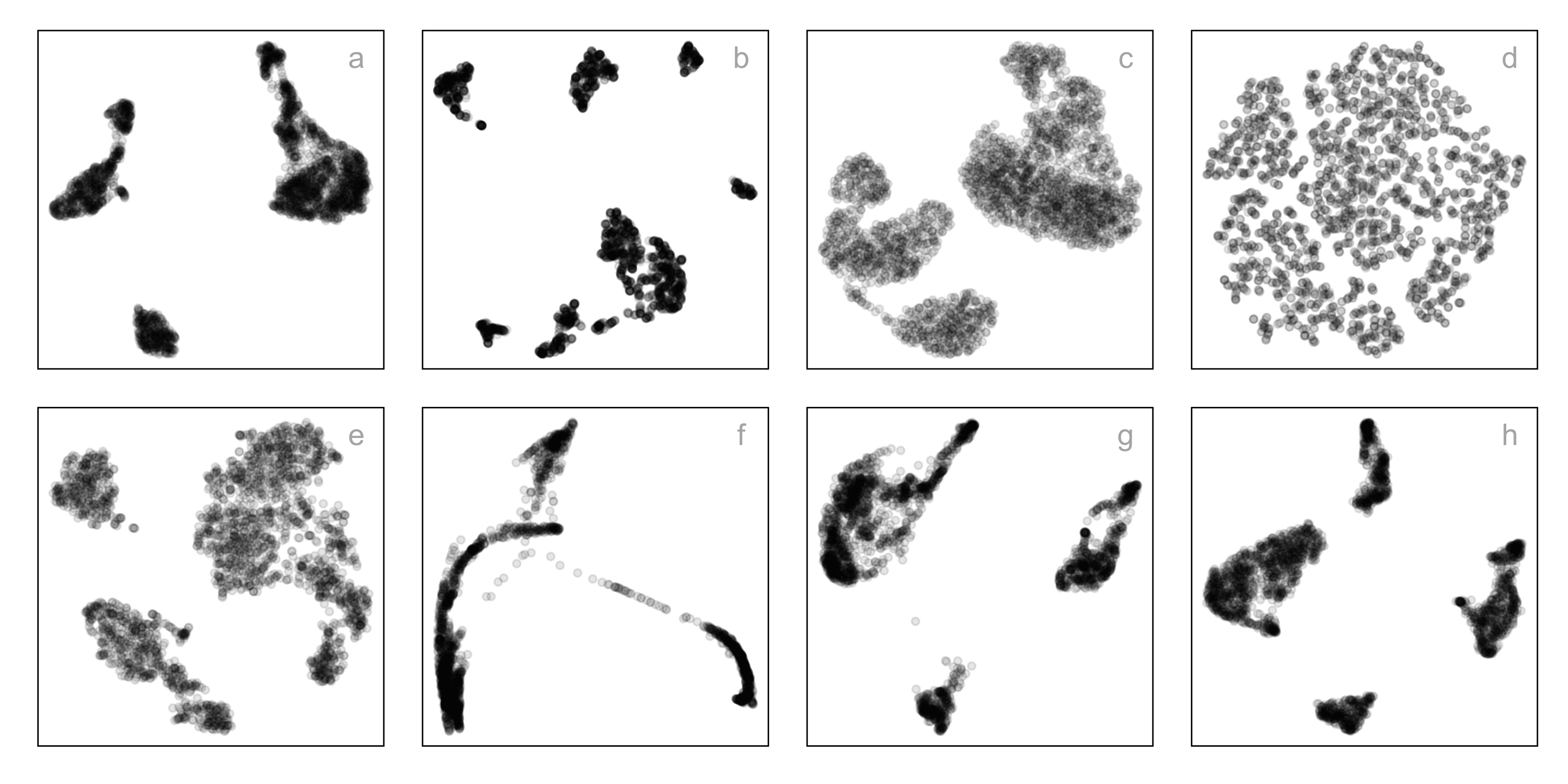
How do you decide which is the most reasonable representation?
This is the published figure.
Here is the 9D data viewed using a grand tour, linear projections into 2D.
Show “model-in-the-data-space”
data-in-the-model-space
model-in-the-data-space
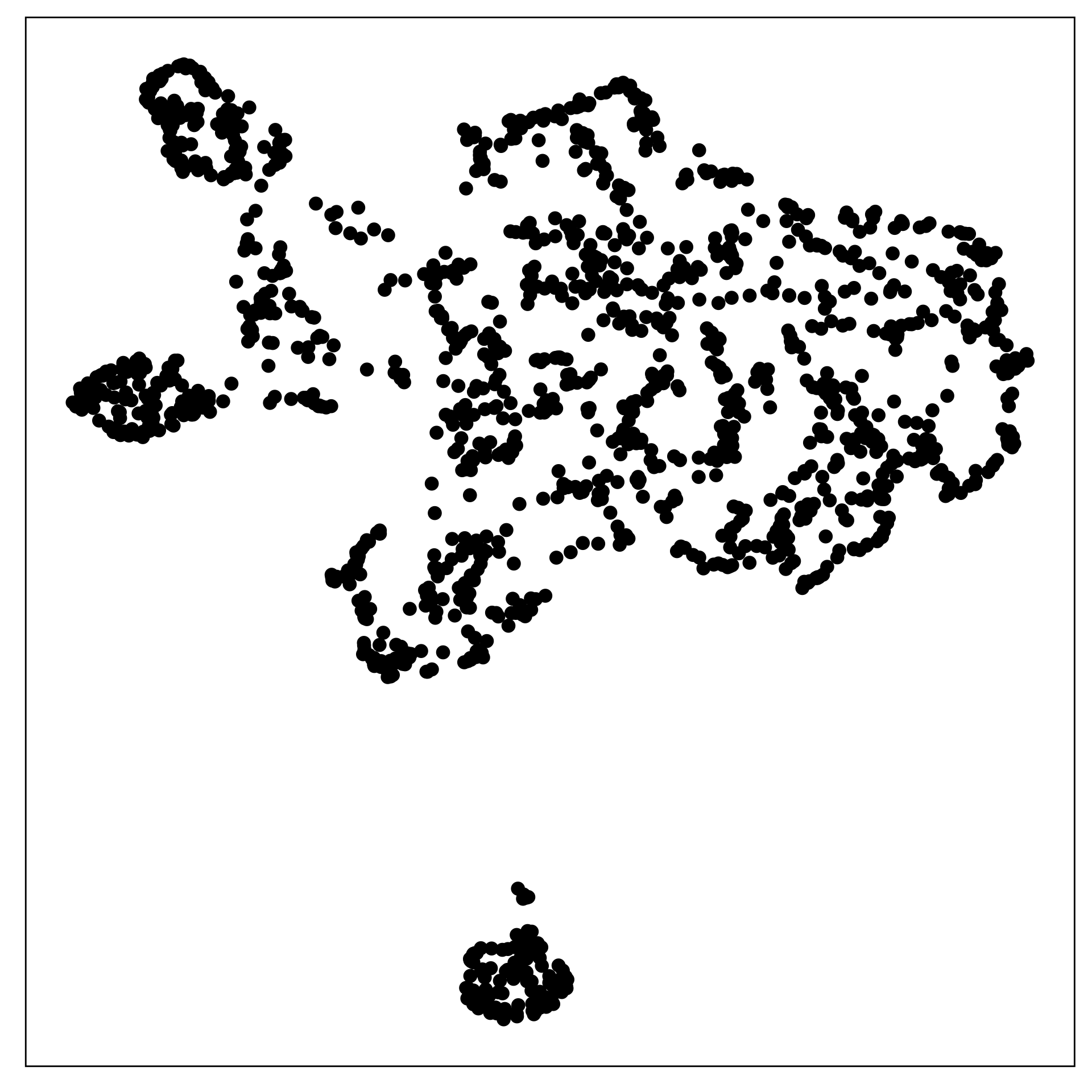
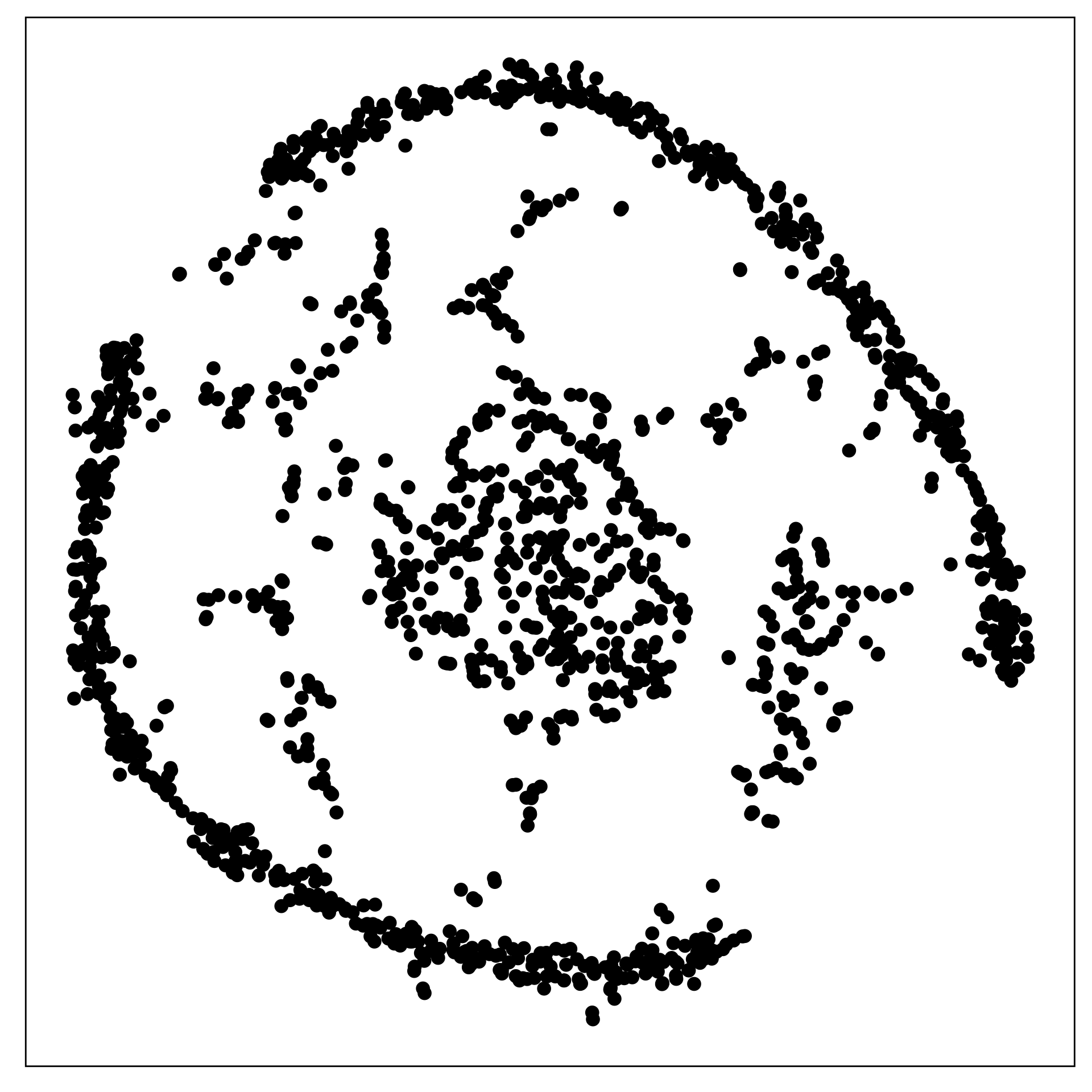
S-curve in 7D
θ∼U(−3π/2,3π/2)
X1=sin(θ)
X2∼U(0,2)
X3=sign(θ)×(cos(θ)−1)
True model: T=(X1,X2,X3)
X4,X5,X6,X7 are additional noise dimensions
data-in-the-model-space
What is the model?
data-in-the-model-space
model-in-the-data-space
Overview of method
1. Construct the 2-D model
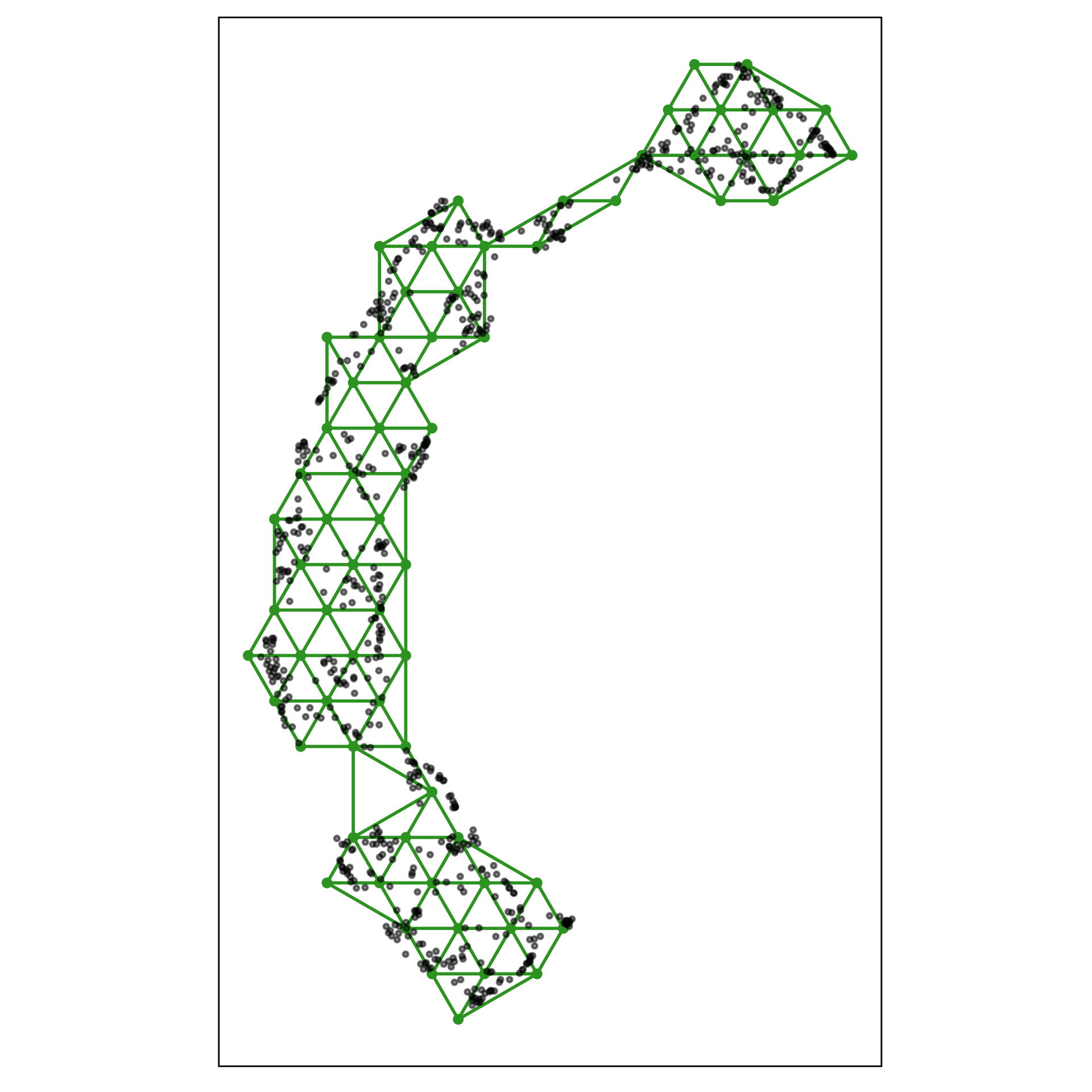
2. Lift the model into high-dimensions
Steps of the algorithm
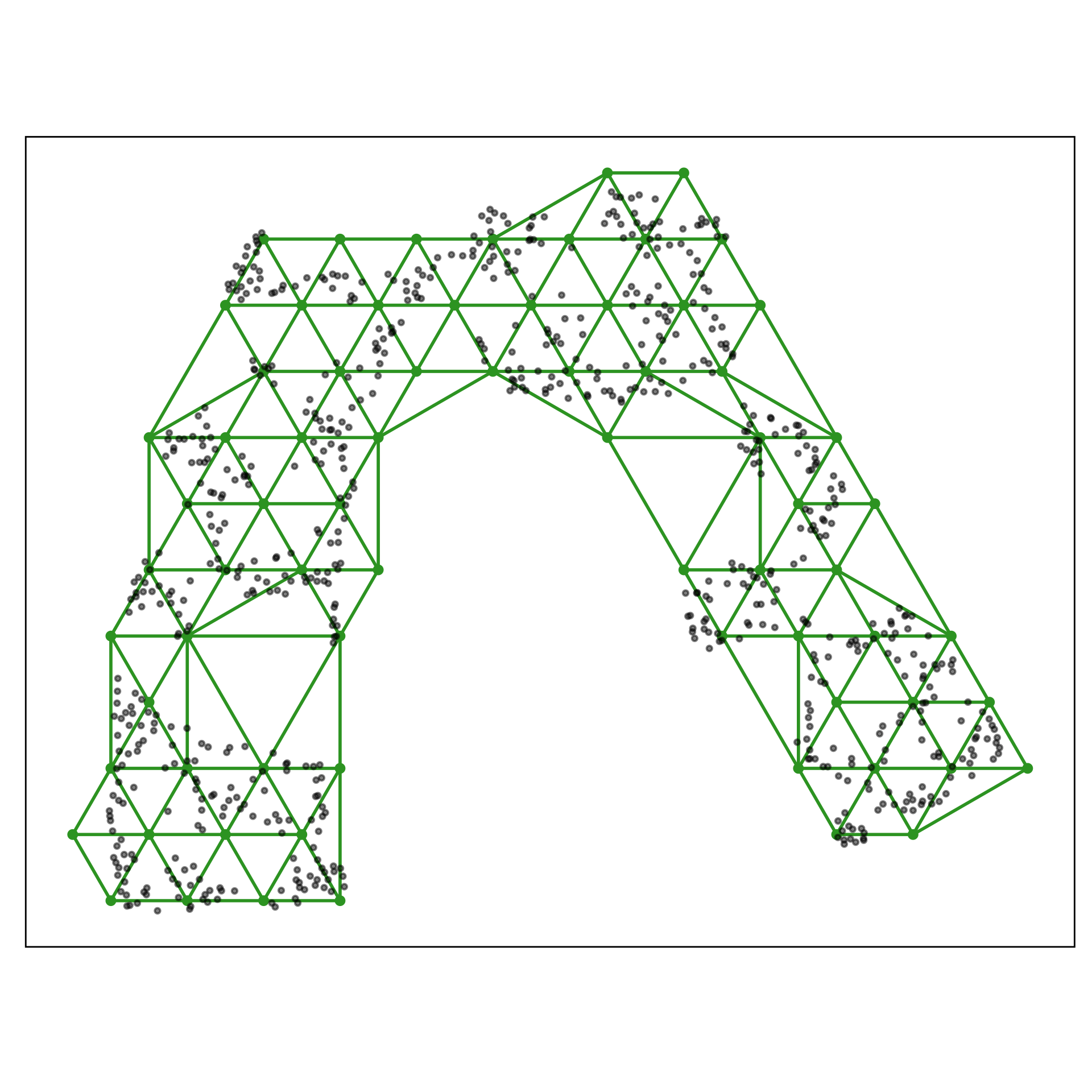
1. Construct the 2-D model
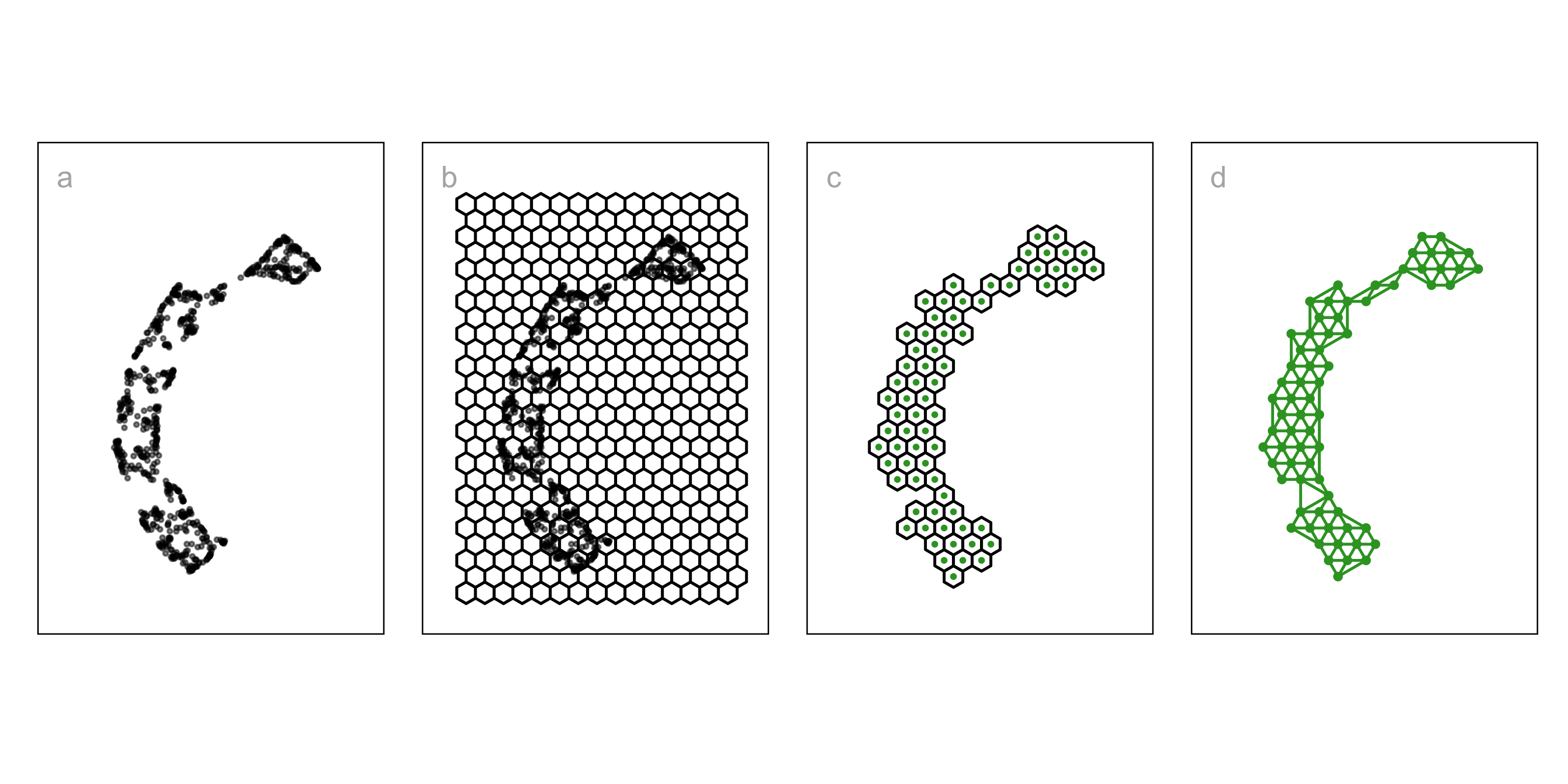
- NLDR layout, b. hex bin , c. bin centers, d. triangulation wire frame.
Steps of the algorithm
2. Lift the model into high-dimensions
Factors for fitting and measuring fit
- NLDR layout, different methods and different hyper-parameters
- Number of bins
- Bin start position
- Low density removal
- Long edge removal
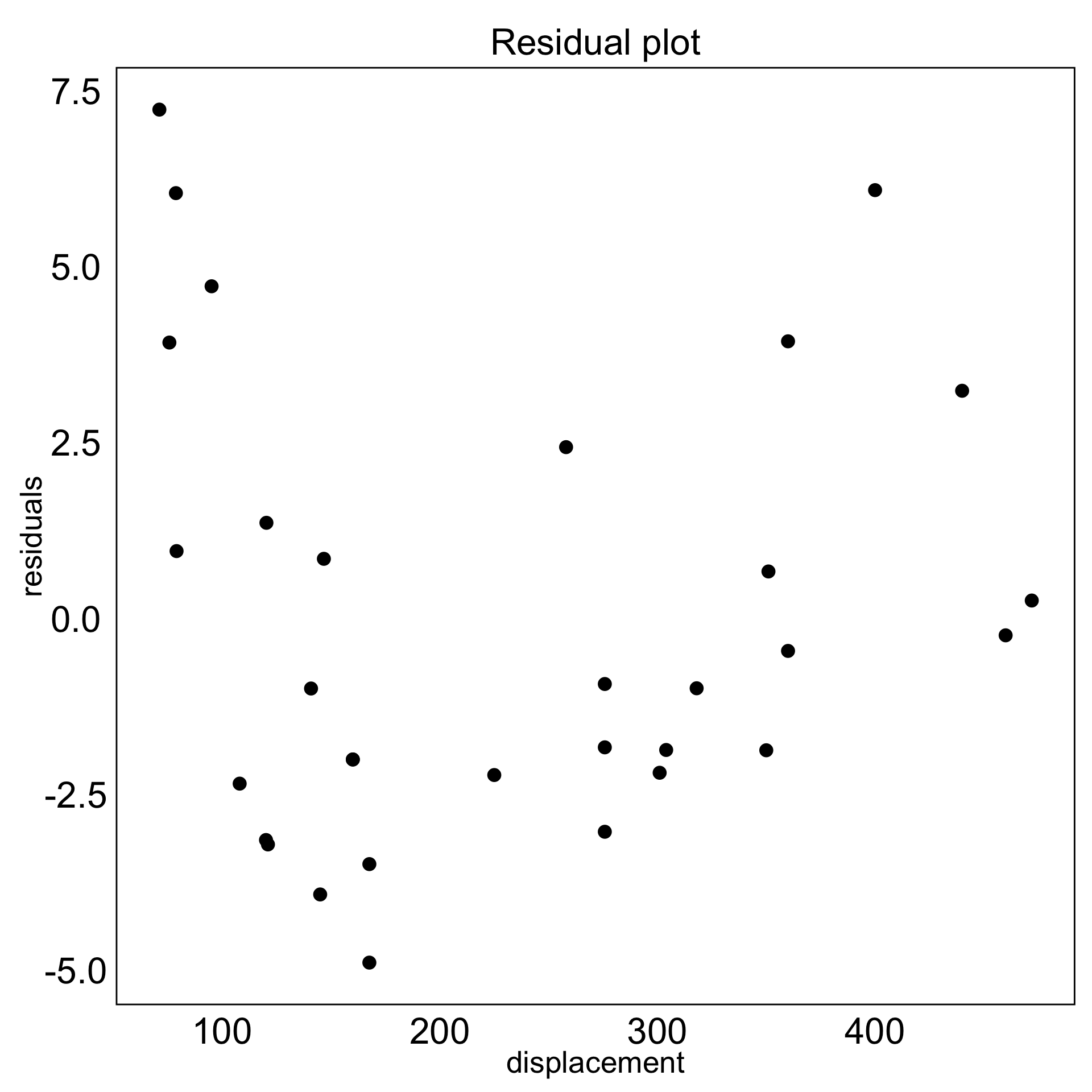
- MSE in high-dimensions: mean sum of squared differences between observed and fitted values
1nb∑h=1nh∑i=1p∑j=1(xhij−C(p)hj)2 n= the number of observations,
b= the number of bins,
nh= the number of observations in hth bin,
p= the number of variables,
xhij= the jth dimensional data of ith observation in hth hexagon.
Candidates for NLDR layout
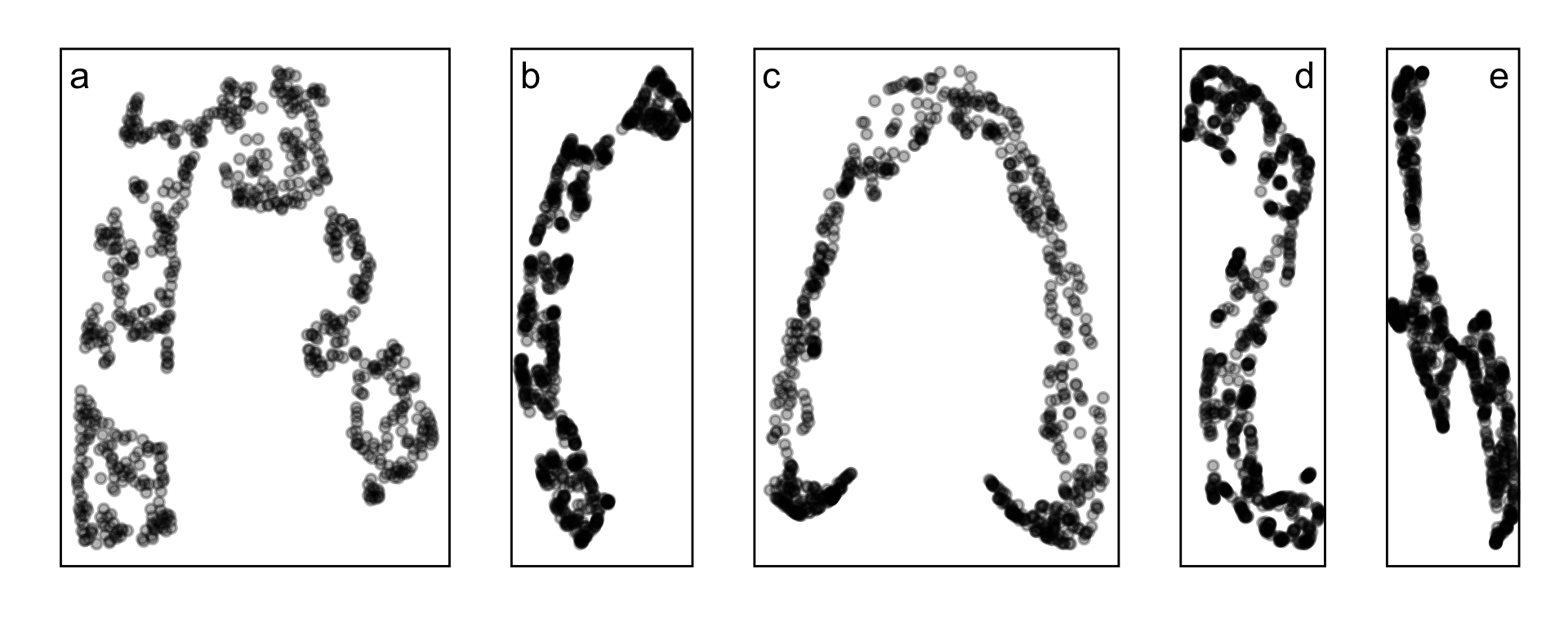
- tSNE, b. UMAP, c. PHATE, d. TriMAP, e. PaCMAP
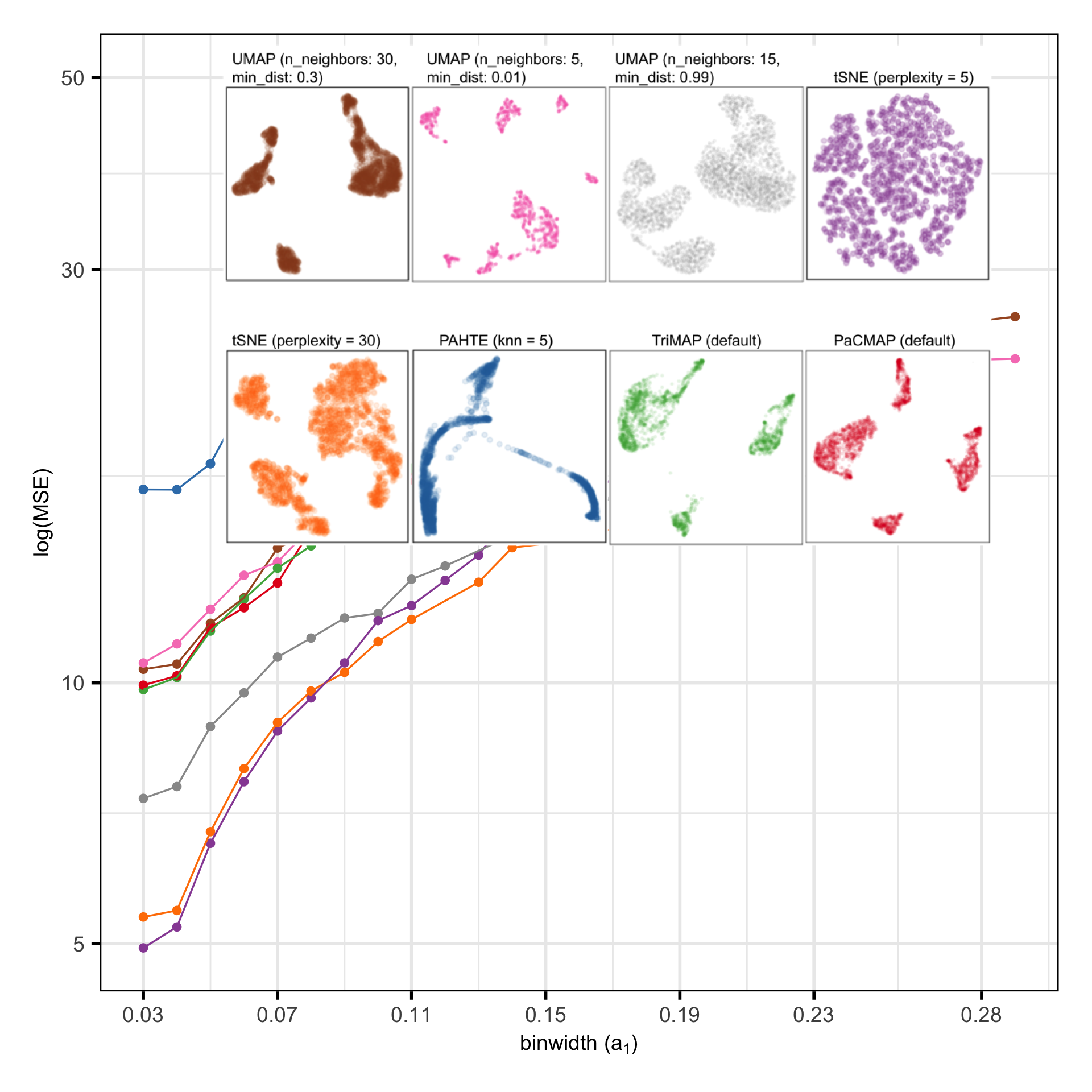
MSE of candidates
- PHATE not competitive
- Not much difference between any other method based on Error
- No elbow, just gradual decrease as number of (non-empty) bins increase
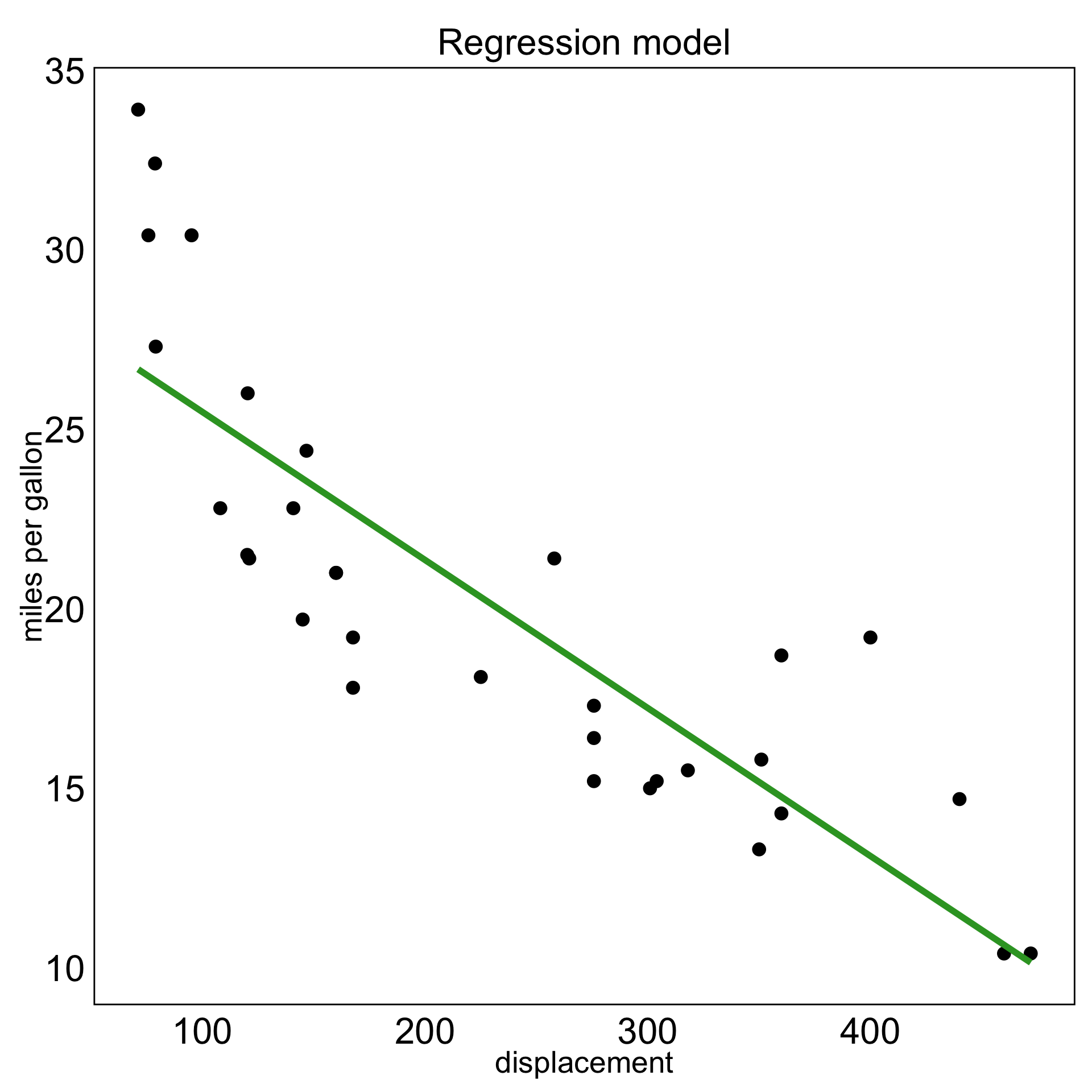
Chosen fit for S-curve
tSNE with perplexity: 27
Fills out the width of the S
Pretty good! Can you see the twist??
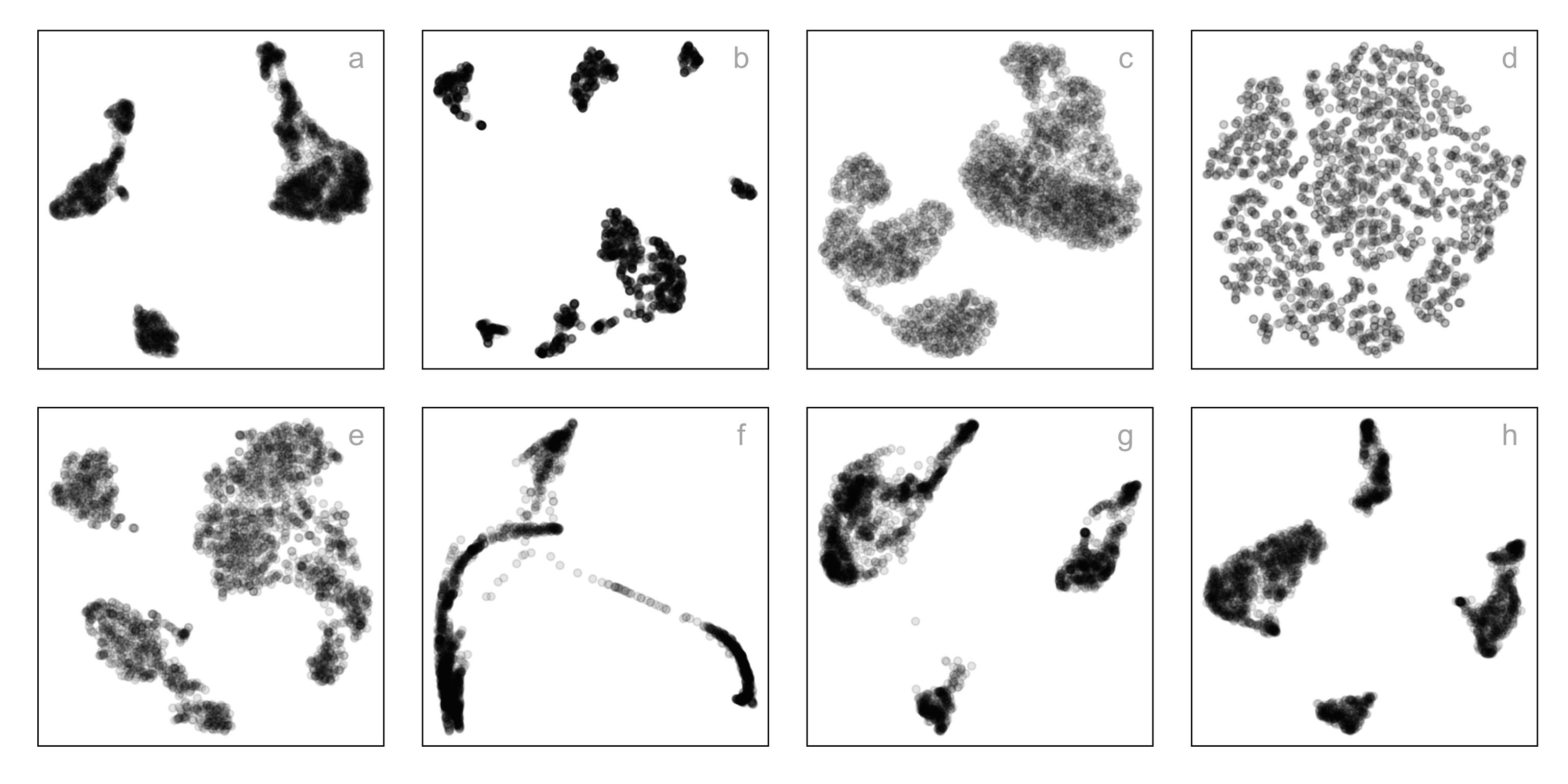
PBMC data set
MSE of candidates
Chosen fit for PBMC data set
tSNE with perplexity: 30
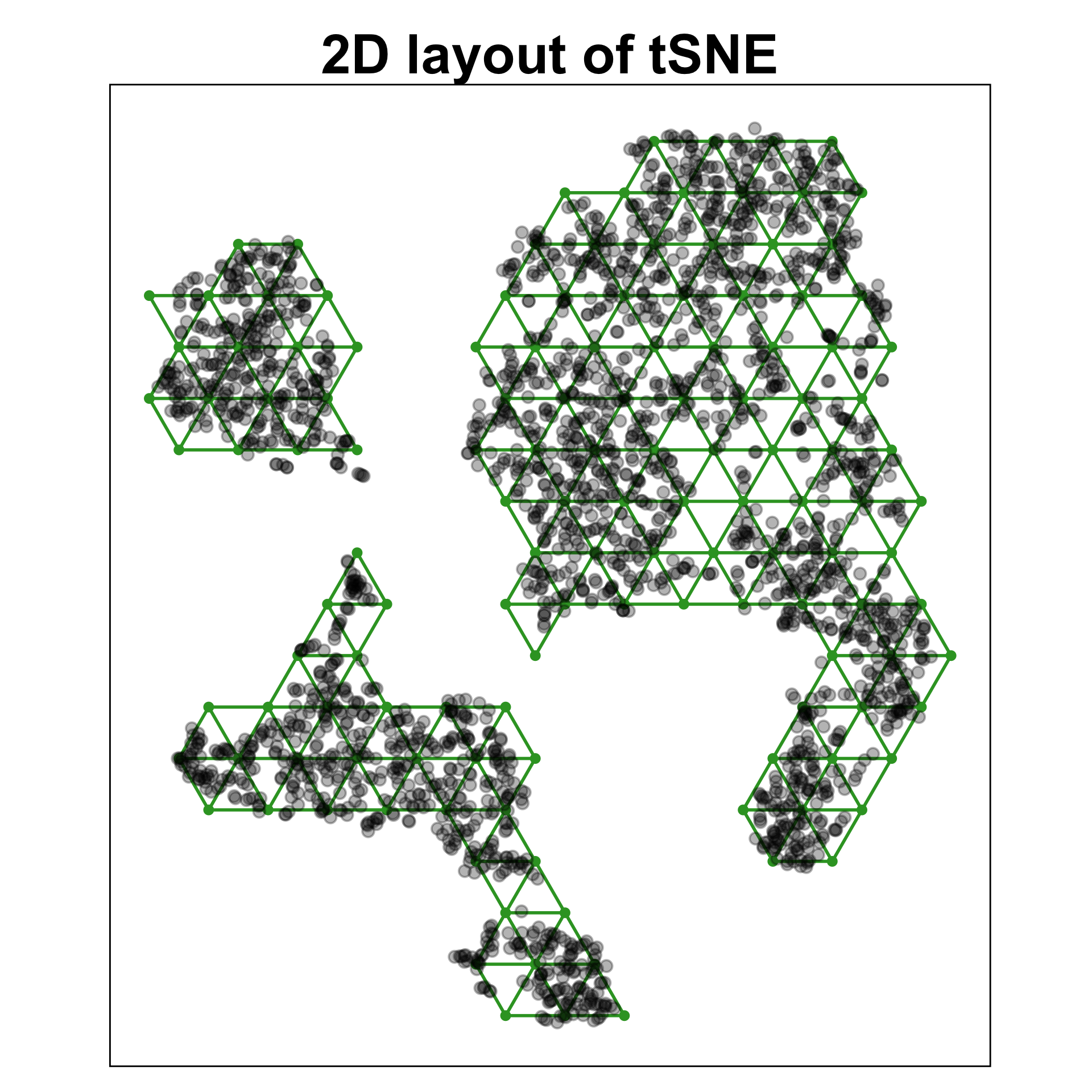
Clusters with small separations, non-linear clusters
Densed points, filled out clusters
Five Gaussian clusters in 4D
tSNE
PaCMAP
Linked plots
- Assess the model fits the points everywhere, better in some places, simply mismatches the pattern
quollr
questioning how a high-dimensional object looks in low-dimensions using r
Summary
Note
- Provided a method to create a model from a NLDR layout that can be displayed with the data to assess the fit.
- Make it easier for researchers to make better decisions on which NLDR layout is best for their work.
Jayani P.G. Lakshika 
Collaborators: Prof. Dianne Cook, Dr. Paul Harrison, Dr. Michael Lydeamore, Dr. Thiyanga S. Talagala
Visualising your fitted non-linear dimension reduction model in the high-dimensional data space Jayani P.G. Lakshika Joint work with Prof. Dianne Cook, Dr. Paul Harrison, Dr. Michael Lydeamore, Dr. Thiyanga S. Talagala